Moment (Central Moments of a Value)

The Moment instruction is used to output the mathematical central moments of a value over the output interval.

Syntax

Moment ( Reps, Source, Order, DataType, DisableVar )

Remarks

This instruction is intended for use on a sample data set rather than a random variable in mathematical statistics theory. Each moment represents a measurement of a particular feature of a random variable that the sample data set represents. Users should be aware that this instruction can be very process intensive for certain applications and considerations on variable data types should be made. 

Definitions of common terms, equations and outputs of the instruction:

Probability Function:  The dispersion of values in a data set represents the probability distribution function.  These functions exhibit particular characteristics, which can be studied when calculating the moments of the distribution function.

Sample Mean: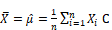 Central Moment: The n-th central moment of a random variable X, no matter discrete or continuous, is defined as the expectation of the n-th power of (X-μ), where μ is the true mean of X:

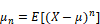
The 2nd Central Moment, the variance, is a measure of the dispersion of a distribution. When considering a normal distribution this value is visually represented by the width of the distribution. The square root of the variance is the standard deviation (σ).

The 3rd Central Moment is used to calculate the Skewness. Skewness is a measure of the degree of asymmetry of a distribution, and is defined as:

.

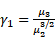The 4th Central Moment is used to calculate Excess Kurtosis. Excess Kurtosis is the degree of peakness of a distribution, and is defined as:

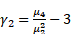
However, while dealing with the sample data, some corrections need to be made on the previous mentioned equations. For a sample data set of size n under assumption of equal probability on each observed value:

Sample Variance: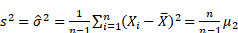

Sample Skewness: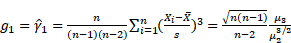

Sample Excess Kurtosis: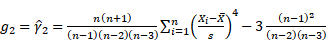

 

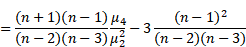
Orders 2 through 5 are supported by this instruction.

Parameters

Reps (Repetitions)

The number of variables for which to calculate a moment (a separate Moment will be calculated for each variable). If the Reps parameter is greater than 1, an array must be specified for Source. If not, a Variable out of Bounds error will be returned when the program is compiled.

Type: Variable

Source

The name of the Variable that is the input for the instruction. Right-click the parameter to display a list of defined variables.

Type: Variable

Source may also be an expression. The resulting fieldname is AnonymousN, where N is an incrementing number assigned to each output value entered as an expression. The FieldNames instruction can then be used to change AnonymousN to a more appropriate fieldname; for example,

Sample (1,PTemp*1.8+32,FP2)

FieldNames("PTempDegFSample:Sample Panel Temp in degrees F")

Order

The order of polynomial to be used when calculating the moment. The following options are valid:

Order	Description
2	Average over i (x(i) - Mean)^2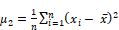
3	Average over i (x(i) - Mean)^3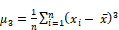
4	Average over i (x(i) - Mean)^4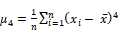
5	Average over i (x(i) - Mean)^5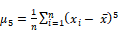

DataType

A code to select the data storage format.  Right-click the parameter to display a list.

Name	Description
IEEE4	IEEE four-byte floating point (IEEE 754 std). IEEE4 can also be specified using the keyword FLOAT.
FP2	Campbell Scientific two-byte floating point.
IEEE8	IEEE eight-byte floating point (double)

Additional data types are available. However, not all data types are suitable for all output instructions, so they should be used with care.

Name	Description
String	ASCII string; size defined by program
Boolean	0 = False; -1 = True
BOOL8	1-byte Boolean value
Long	32-bit long integer, ranging from -2,147,483,648 to +2,147,483,647
NSEC	8-byte time stamp format
UINT1	One-byte unsigned integer
UINT2	Two-byte unsigned integer
UINT4	Four-byte unsigned integer

UINT1: Holds an 8-bit unsigned integer (a number in the range of 0 - 32,767, where NAN values are stored as 0). The program should be written to check for values outside the range. This data type is an efficient means of storing 8-bit integers since it requires only one byte of memory in a data table. Floating point values are converted to UINT1 as if the INT function were used.

UINT2: Holds a 16-bit unsigned integer (a number in the range of 0 - 65535, where NAN values are stored as 0). The program should be written to check for values outside the range. This data type is an efficient means of storing 16-bit integers since it requires only two bytes of memory in a data table. Floating point values are converted to UINT2 as if the INT function were used.

UINT4: Holds a 32-bit unsigned integer (a number in the range of 0 to 4,294,967,295).

Long: Sets the output to a 32-bit long integer, ranging from -2,147,483,648 to +2,147,483,647 (31 bits plus the sign bit). There are two possible reasons a user would use this format: (1) speed, since the OS can do math on integers faster than with floats, and (2) resolution, since the Long has 31 bits compared to the 24-bits in the IEEE4. However, in most instances it is not suitable for output since any fractional portion of the value is lost.

BOOL8: Used to store variables that hold bits (0 or 1) of information. These values are shown in LoggerNet or other datalogger software as an array of eight Boolean values (each element in the array represents one bit). This data type uses less space than normal 32-bit values. Any reps stored must be divisible by two, since an odd number of bytes cannot be stored in a data table. When converting from a Long or a Float to a BOOL8, only the least significant 8 bits are used.

NSEC: An 8-byte time stamp format (4 bytes of seconds since 1990, 4 bytes of nanoseconds into the second) used when the variable being sampled is the result of the RealTime instruction or when the variable is a Long storing time since 1990 (for instance, when using TableName.TimeStamp). If the variable array is dimensioned to 7, the values stored will be year, month, day of year, hour, minutes, seconds, and milliseconds. The variable array must be declared as a Float or Long. If the variable array is dimensioned to two and declared as a Long, the instruction assumes that the first element holds seconds since 1990 and the second element holds microseconds into the second. If the source is a single variable dimensioned as a Long, the instruction assumes that the variable holds seconds since 1990 and the microseconds into the second is 0. In this instance, the value stored is a standard datalogger timestamp rather than the number of seconds since January 1990.

Type: Constant (or expression that evaluates as a constant)

DisableVar

A Constant, Variable, or Expression that is used to determine whether the current measurement is included in the output saved to the DataTable. Right-click the parameter to display a list.

• 0 = Process current measurement
• Non-zero = Do not process current measurement.

For all instructions except Totalize, if the disable variable is true over the entire output interval, NAN Not a number. A data word indicating a measurement or processing error. Voltage overrange, SDI-12 sensor error, and undefined mathematical results can produce NAN. will be stored. For Totalize, if the disable variable is true over the entire output interval, 0 will be stored

Multipliers, Offsets, and Disable Variables with Repetitions

Type: Constant, Variable, Expression

For Average, Covariance, Maximum, Minimum, Moment, StdDev, Totalize - if DisableVar is an array and Reps are greater than 1, a different DisableVar can be used for each rep.