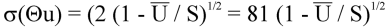Wind Vector Calculations
Measured raw data
-
Si: horizontal wind speed
-
Θi: horizontal wind direction
-
Uei: east-west component of wind
-
Uni: north-south component of wind
-
N: number of samples
Input Sample Vectors
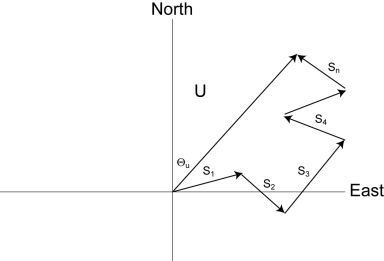
In the preceding image, the short, head-to-tail vectors are the input sample vectors described by si and Θi, the sample speed and direction, or by Uei and Uni, the east and north components of the sample vector. At the end of data storage interval T, the sum of the sample vectors is described by a vector of magnitude U and direction Θu. If the input sample interval is t, the number of samples in data storage interval T is N = T / t. The mean vector magnitude is Ū = U / N.
Scalar mean horizontal wind speed, S:
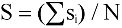
where in the case of orthogonal sensors:
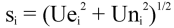
Unit vector mean wind direction,
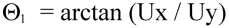
where
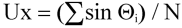
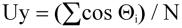
or, in the case of orthogonal sensors
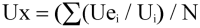
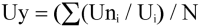
where
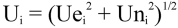
Standard deviation of wind direction (Yamartino algorithm)
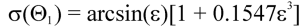
where,
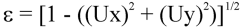
and Ux and Uy are as defined above.
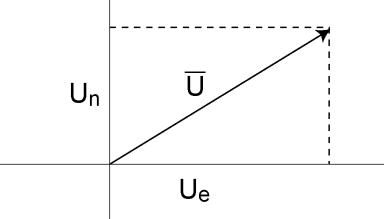
Mean Wind Vector
Resultant mean horizontal wind speed, Ū:
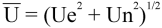
where for polar sensors:
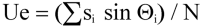
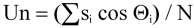
or, in the case of orthogonal sensors:

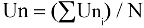
Resultant mean wind direction, Θu:
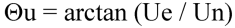
Standard deviation of wind direction, σ (Θu), using Campbell Scientific algorithm:
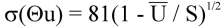
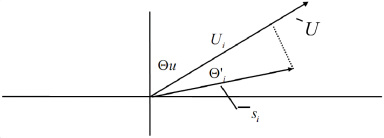
The algorithm for σ (Θu) is developed by noting, as shown in the following image, that
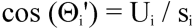
where

The Taylor Series for the Cosine function, truncated after 2 terms is:
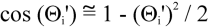
For deviations less than 40 degrees, the error in this approximation is less than 1%. At deviations of 60 degrees, the error is 10%.
The speed sample can be expressed as the deviation about the mean speed,
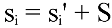
Equating the two expressions for Cos (θ') and using the previous equation for si;
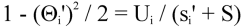
Solving for (Θi')2, one obtains;
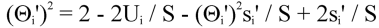
Summing (Θi')2 over N samples and dividing by N yields the variance of Θu.
The sum of the last term equals 0.
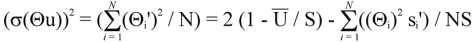
The term,
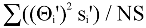
is 0 if the deviations in speed are not correlated with the deviation in direction. This assumption has been verified in tests on wind data by Campbell Scientific; the Air Resources Laboratory, NOAA, Idaho Falls, ID; and MERDI, Butte, MT. In these tests, the maximum differences in
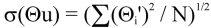
and
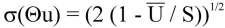
have never been greater than a few degrees.
The final form is arrived at by converting from radians to degrees (57.296 degrees/radian).